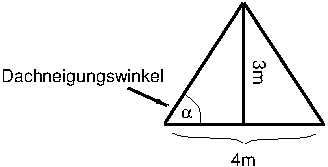In der Trigonometrie werden die Beziehungen zwischen Seiten und Winkeln von Dreiecken untersucht, welche man zum Beispiel für die Berechnung von Entfernungen, Navigation, Winkeln und Schrägen benötigt. Für trigonometrische Funktionen gibt es außerdem Anwendungen bei der Modellierung von Wellen (Schallwellen, elektromagnetischen Wellen, Radiowellen, Herzrhythmen usw.).
Winkel kann man in Grad messen oder auch als Länge eines Kreisbogens. Aus der Geometrie ist bekannt, dass der Umfang eines Kreises 2πr beträgt, wobei r der Radius ist. Somit gilt im Einheitskreis (d.h. bei einem Kreis mit Radius 1), dass der Umfang 2π beträgt. Ein 90° Winkel teilt einen Kreis in 4 Viertel, welches im Einheitskreis einem Bogenmaß von 2π/4=π/2 entspricht. Das folgende Bild zeigt weitere Beispiele von Winkeln und deren Grad- und Bogenmaß im Einheitskreis.

Trigonometrie beruht darauf, dass es in einem rechtwinkligen Dreieck feste Beziehungen zwischen Längen und Winkeln gibt. In einem rechtwinkligen Dreieck wird die Seite, die gegenüber dem rechten Winkel liegt, als Hypotenuse bezeichnet. Die anderen beiden Seiten heißen Katheten. Die Kathete gegenüber einem betrachteten Winkel α heißt Gegenkathete, die andere Ankathete. (Da die Trigonometrie schon vor mehr als 2000 Jahren erfunden wurde, sind die Bezeichnungen griechisch).
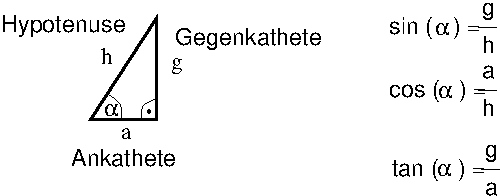
In einem rechtwinkligen Dreieck gelten für den Winkel α mit den Bezeichnungen wie im obigen Bild die Beziehungen:
Zeigen Sie, dass sin(α)/cos(α) = tan(α) gilt.
Man kann ein rechtwinkliges Dreieck so in einen Einheitskreis zeichnen, dass die Hypothenuse dem Radius entspricht (d.h. Länge 1 hat). Dabei gibt es die Extremfälle für α = 0°, α = 90°, α = 180° und α = 360°, bei denen die drei Seiten des Dreiecks aufeinander fallen. In den Extremfällen ist dann jeweils einer der Werte (cos oder sin) gleich 0 und der andere gleich 1 oder -1. Ansonsten sind die Werte von cos und sin zwischen -1 und 1.
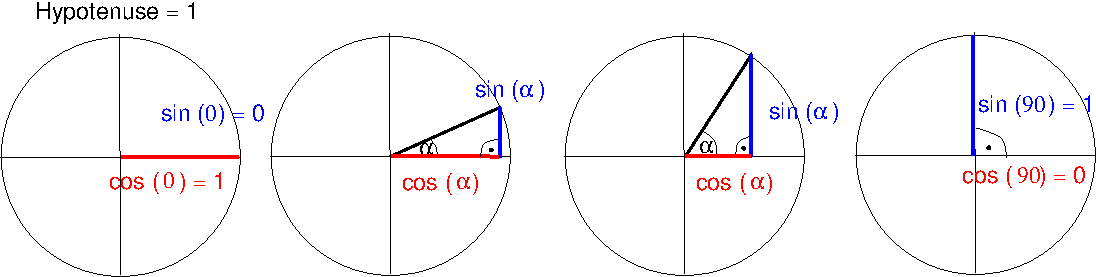
1. Überlegen Sie sich anhand des Bilds, welche Werte sin und cos abhängig von α ungefähr annehmen.
Die Werte für einige Winkel (im Bogenmaß und Gradmaß) stehen in dieser Tabelle:
| α | 0 | π/6 | π/4 | π/3 | π/2 |
|---|---|---|---|---|---|
| 0° | 30° | 45° | 60° | 90° | |
| sin(α) | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos(α) | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan(α) | 0 | √3/3 | 1 | √3 | - |
1. Überprüfen Sie die Tangenswerte aus der Tabelle anhand der Formel sin(α)/cos(α) = tan(α).
2. Wenn Sie sich noch an Geometrie aus der Schule erinnern, können Sie die Werte für 30° und 60° bestimmen, indem Sie das Dreieck zu einem gleichseitigen Dreieck ergänzen und dann den Satz des Pythagoras anwenden.
3. Was passiert bei Winkeln größer als 360° oder kleiner als 0°?
4. Wieso ist der Tangens von 90° nicht definiert?
Der Kehrwert des Tangens wird als Kotangens bezeichnet: cot(α) = 1/tan(α). Man kann den Tangens und Kotangens auch am Einheitskreis visualisieren. Um genau zu verstehen, warum das folgende Bild richtig ist, müssen Sie aber aus der Geometrie wissen, wie man ähnliche Dreiecke erkennt (d.h. mit gleichen Winkeln und gleichen Seitenverhältnissen). Die trigonometrischen Werte sind in ähnlichen Dreiecken gleich.
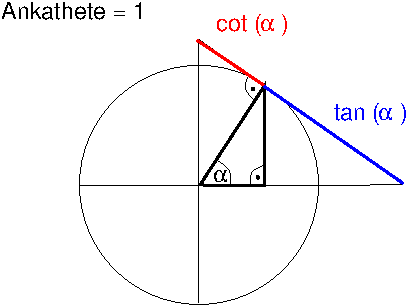
1. Überlegen Sie nochmal anhand des Bilds, wieso der Tangens von α = 90° nicht definiert ist.
2. Welcher Kotangenswert ist nicht definiert?
3. Was passiert mit den Werten von Tangens und Kotangens, wenn der Winkel α größer oder kleiner wird?
Um sin, cos und tan in Python zu berechnen, müssen Sie die Werte im Bogenmaß angeben:
Werte im Gradmaß können Sie mit radians in Bogenmaß umwandeln. Werte im Bogenmaß können Sie mit degrees in Gradmaß umwandeln.
Die Funktionen lassen sich auch alle umkehren und heißen dann asin, acos und atan (ausgesprochen als Arkussinus usw.). Wenn Sie also einen Wert für sin, cos oder tan kennen, können Sie das jeweilige Bogen- oder Gradmaß berechnen:
Für die Kehrwerte des Sinus und Kosinus gibt es auch Bezeichnungen, die aber selten verwendet werden. Außerdem gibt es noch einige Formeln und Rechenregeln, die Sie nachschlagen können, falls Sie sie brauchen und die hier nicht weiter erläutert werden.
1. Für welche Winkel ist der Sinus/Kosinus jeweils positiv oder negativ? Welche Werte kann der Tangens annehmen (ist der auch zwischen -1 und 1)?
2. Wieso gilt (sin(α))2 + (cos(α))2 = 1?
Zumindest im Einheitskreis
ist das leicht mithilfe des Satz des Pythagoras zu sehen. Zeigen Sie, dass die Gleichung
auch dann gilt, wenn die Hypotenuse nicht gleich 1 ist, indem Sie die Formeln, mit denen
sin und cos definiert sind, in den Satz des Pythagoras einsetzen.
3. Berechnen Sie, in welchem Winkel zum Dach Sie Photovoltaik-Module auf dem abgebildeten Dach anbringen müssen, wenn die Module einen Neigungswinkel von 48° haben sollen (also etwas flacher geneigt als das gezeigte Dach). Rechnen Sie geometrisch und trigonometrisch und überprüfen Sie dann mit einem Winkelmesser (den Sie vermutlich aus Ihrer Schulzeit noch haben).