Hier ist ein Quiz, mit dem Sie Kenntnisse in diesem Gebiet überprüfen können. Sie sollten die Aufgaben ohne Taschenrechner durch Anwenden von Rechenregeln lösen können.
Hier nochmal die Bezeichnungen für Potenzen und Wurzeln:
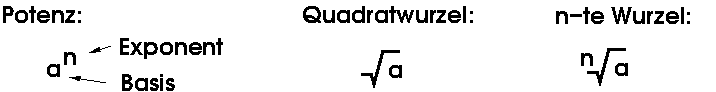
Potenz-, Wurzel- und Logarithmenrechnung stehen in einem engen Zusammenhang, da es sich um 3 Sichtweisen der gleichen Beziehung handelt:

Zum Beispiel: $4^3 = 64$ $\sqrt[3]{64} = 4$ $64^{1/3} = 4$ $log_4(64) = 3$.
Anstatt $\sqrt[n]{b}$ kann man auch $b^\frac{1}{n}$ schreiben. Daher lassen sich die Regeln für Wurzeln direkt aus den Regeln für Potenzrechnung herleiten.
| $\mbox{Potenzen}$ | $\mbox{Wurzeln}$ |
| $a^n * b^n = (ab)^n$ | $\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}$ |
| $a^n / b^n = (a/b)^n$ | $\sqrt[n]{a}$ / $\sqrt[n]{b}=\sqrt[n]{a/b}$ |
| $a^n * a^m = a^{n + m}$ | $\sqrt[n]{a}\sqrt[m]{a}=a^{\frac{1}{n} + \frac{1}{m}}$ |
| $a^n / a^m = a^{n - m}$ | $\sqrt[n]{a}$ / $\sqrt[m]{a}=a^{\frac{1}{n} - \frac{1}{m}}$ |
| $(a^n)^m = a^{n*m}$ | $\sqrt[m]{\sqrt[n]{a}} = \sqrt[nm]{a}$ |
Man kann sich die Regeln veranschaulichen, wenn man sich klar macht, dass der Exponent die Anzahl der Faktoren zählt. Dabei kann man die Faktoren umsortieren und anders zählen. Statt a und b sind die Variablen hier als Smileys dargestellt:
😀😀😀 * 😈😈😈 = (😀😈)* (😀😈)*(😀😈)
😀😀😀 * 😀😀 = 😀😀😀😀😀
(😀😀😀)2 = 😀😀😀 * 😀😀😀 = (😀😀)3
Welche der 5 Regeln sind durch die Smileys dargestellt?
Die Regeln lassen sich durch Umformungen erklären. Überlegen Sie sich, was jeweils dort stehen muss oder erklärt werden muss, wo in den folgenden Zeilen das Wort "Umformung" steht. Falls es Ihnen nicht klar ist, setzen Sie Werte für $n$ und $m$ ein und schreiben Sie die Formeln dafür hin.
$a^n * b^n = a * \ldots * a * b * \ldots * b =$ Umformung $= (ab)^n $
$a^n * a^m =$ Umformung $= a^{n + m}$
$(a^n)^m =$ Umformung $= a^{n*m}$
$\sqrt{a}\sqrt{a}=$ Umformung $=a$
In Python ist die Schreibweise für Exponenten **, z.B. $4^3$ wird als 4**3 geschrieben. Es gibt in Python eine Funktion für Quadratwurzeln (sqrt(), da Wurzel auf Englisch square root heißt). Für n-te Wurzeln kann man mit **(1/n) zu rechnen. Python nähert die Werte dann aber eventuell nur an. Rechnen Sie erst auf Papier durch Anwendung von Regeln und in mathematischer Schreibweise, bevor Sie sich die Lösungen ansehen.
Für welche Werte von $n$ gilt $(-1)^n = 1$ und für welche gilt $(-1)^n = -1$?
Mit Variablen rechnen:
Wurzeln:
sqrt(49) liefert im CAS nur ein Ergebnis, obwohl sowohl $7^2 = 49$ als auch $(-7)^2 = 49$. Quadratwurzeln aus negativen Zahlen ergeben komplexe Zahlen, die in diesem Vorkurs nicht weiter behandelt werden. Für eine ungerade Zahl $n$ ist die n-te Wurzel aus einer negativen Zahl eine reelle Zahl, z.B. $\sqrt[3]{-27} = -3$, d.h., das können Sie berechnen, aber nicht unbedingt mit einem CAS (NaN bedeutet: not a number).
Man kann auf die Bruchrechnung komplett verzichten, wenn man mit negativen Potenzen rechnet. Anstatt $\frac{1}{n}$ kann man nämlich auch $n^{-1}$ schreiben.
1. Erklären Sie das Ergebnis für $3^0$ mit Hilfe der Rechenregeln für $3^{2-2}$ und indem Sie $3^{-2}$ als $\frac{1}{3^2}$ schreiben:
2. Schreiben Sie diese Beispiele ohne Potenzen als reine Bruchrechnung und erklären Sie die Regeln der Bruchrechnung mit den Regeln der Potenzrechnung:
Falls Sie sich nicht sicher sind, überprüfen Sie einzelne Schritte mit dem CAS.
Bei Logarithmen kennt man die Basis und das Ergebnis und sucht den Exponenten. Wenn Sie zum Beispiel die Potenzen von 2 betrachten (1, 2, 4, 8, 16, ...), können Sie durch Ausprobieren den Exponenten bestimmen, den man braucht um 256 zu erhalten. Die Zahl 2 wird dabei als Basis bezeichnet, die Zahl 256 als Argument oder Numerus bezeichnet.
Das Argument 64 können Sie sogar als Potenz verschiedener Basen darstellen:
Man bezeichnet das Finden des Exponenten als Logarithmieren. In Python verwendet man dafür $log(a,b)$, wobei $a$ das Argument ist und $b$ die Basis.
Dabei müssen a und b reelle Zahlen sein, die größer als 0 sind und b darf auch nicht 1 sein. Aufgabe: überlegen Sie sich, warum b nicht 1 sein darf.
Berechnen Sie die folgenden Werte. Rechnen Sie wieder erst, bevor Sie sich die Lösungen ansehen:
Die Regeln für das Rechnen mit Logarithmen ergeben sich aus den Rechenregeln für Potenzen.
| $\mbox{Potenzen}$ | $\mbox{Logarithmen}$ |
| $b^{log_b(k)} = k$ | |
| $b^n * b^m = b^{n + m}$ | $log_b(nm) = log_b(m) + log_b(n)$ |
| $b^n / b^m = b^{n - m}$ | $log_b(n/m) = log_b(n) - log_b(m)$ |
| $(b^n)^m = b^{n*m}$ | $log_b(m^k) = k * log_b(m)$ |
| $b^0=1$ | $log_b(1) = 0$ |
| $b^1=b$ | $log_b(b) = 1$ |
| $b^k=b^k$ | $log_b(b^k) = k$ |
Zum Beispiel gilt die zweite Zeile, da $nm=b^{log_b(nm)}=
b^{log_b(m)+log_b(n)} = b^{log_b(n)} * b^{log_b(m)} = nm$.
Die Gültigkeit der letzten drei Zeilen sollten Sie erklären können.
Bevor es Computer gab, war das Rechnen mit Logarithmen extrem wichtig, weil man damit zum Beispiel Berechnungen für große Zahlen durchführen und Wurzeln ziehen konnte. Das Rechnen mit Logarithmen war aber auch sehr mühsam, weil man viele Schritte von Hand ausführen musste und dabei Werte in speziellen Logarithmentafeln ablesen musste. Dafür mussten man auch Logarithmen auf die jeweils gewünschte Basis umrechnen. Die Formel für die Umrechnung von einer Basis $b$ auf eine Basis $c$ ist:
Für Logarithmen gibt es viele Anwendungen, da es technische und natürliche Prozesse gibt, die sich gut damit beschreiben lassen. Für die wichtigsten Basen kann man Logarithmen in Python noch einfacher schreiben: log10(n) ist der Logarithmus zur Basis 10, also das Gleiche wie log(n,10) und log2(n) ist der Logarithmus zur Basis 2. Außerdem ist log(n) ohne Angabe einer Basis der Logarithmus zur Basis e. Die Zahl e wird aber in diesem Vorkurs nicht weiter behandelt.
Dabei sehen Sie, dass log10 angibt, wie oft der Faktor 10 im Argument steckt. Man kann damit feststellen, wie viele Stellen eine Zahl hat (nämlich log10 abgerundet + 1). Wie viele Stellen hat zum Beispiel die Zahl 122243242525043503: