In dem folgenden Quiz können Sie Vorkenntnisse in diesem Gebiet überprüfen. Wenn Sie die Begriffe "assoziativ", "kommutativ", "distributiv" und "binomische Formeln" schon gut kennen, brauchen Sie diese Seite nicht weiter zu bearbeiten.
Das Kommutativgesetz gilt für Operationen, bei denen man die Operanden vertauschen darf.
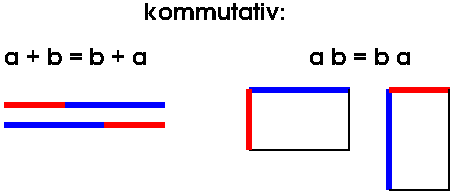
Überlegen Sie erst, bevor Sie die folgenden Rechnungen ausführen, ob jeweils true oder false herauskommt.
Das Assoziativgesetz gilt für Operationen, bei denen man Klammern beliebig setzen darf.
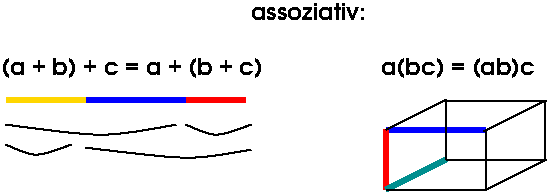
Das Distributivgesetz gilt für zwei verschiedene Operationen, bei denen man "ausklammern" darf.
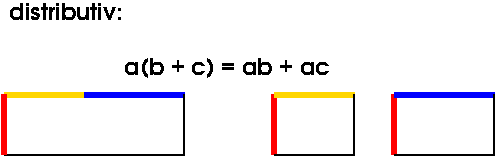Bei nicht kommutativen Operationen gibt es 2 mögliche Distributivgesetze,
die nicht unbedingt beide gelten:
(Bei der letzten Gleichung müssen Sie ein Zeichen ändern, so dass true
herauskommt. Aber dann ist es kein Distributivgesetzt mehr.)
Die Binomischen Formeln ergeben sich unmittelbar aus den oben genannten Rechengesetzen (insbesondere dem Distributivgesetz).
(a + b)2 = a2 + 2ab + b21. Rechnen Sie nach, dass die Binomischen Formeln stimmen. Zum Beispiel: (a + b)2 = (a + b)(a + b)= a(a + b) + b(a + b) = ...
2. Versuchen Sie nachzuvollziehen, wie die ersten beiden Binomischen Formeln hier geometrisch dargestellt sind:
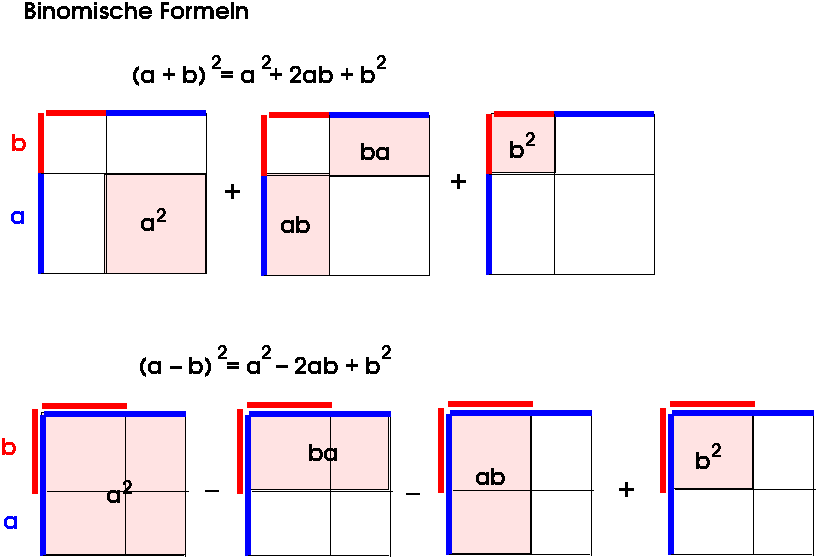
Helfen Ihnen eigentlich die Visualisierungen in diesem Kurs oder finden Sie sie eher verwirrend? Auch wenn es vielleicht zunächst schwer fällt, ist es oft wichtig, sich mathematische Begriffe mental auf unterschiedliche Weisen vorzustellen, damit man sie in unterschiedlichen Zusammenhängen anwenden kann.
Hier folgt ein Quiz, in dem Sie das Verstehen von Visualisierungen noch weiter üben können. Es handelt sich dabei um Standardbeispiele aus der Geometrie, die leicht im Internet zu finden sind, falls Sie sie nicht kennen und 2 Reihen, die beim Thema über Folgen und Reihen noch weiter erläutert werden.