
Bei Gleichungen ist es oft so, dass genau 2 Variablen x und y verwendet werden, die in einer festen Beziehung zueinander stehen, so dass man, wenn man x kennt, dadurch einen Wert für y berechnen kann. Zum Beispiel:
y = x2Anstatt y kann man in solchen Fällen auch f(x) schreiben:
f(x) = x2Man nennt einen Prozess, der jedes Element x einer Menge D (die sogenannte Definitionsmenge) eindeutig in ein Element f(x) einer Menge W (die sogenannte Wertemenge) transformiert auch Funktion und schreibt f: D → W
In Python sind viele Funktionen schon vordefiniert. Beschreiben Sie für die folgenden Funktionen, was deren Zweck wohl ist.
1. Bestimmen Sie für die obigen Python-Funktionen die Definitionsmengen (d.h. auf was für Elemente kann man die Funktionen anwenden) und die Wertemengen (d.h. was für Elemente kommen jeweils heraus)? Zum Beispiel darf man die Wurzelfunktion nur auf positive Zahlen anwenden und es kommen auch nur positive Zahlen heraus.
2. Wenn man Funktionen auf Elemente anwendet, die nicht in der Definitionsmenge liegen, produzieren Programmiersprachen einen Fehler. Überlegen Sie für die nächsten Beispiele erst, welche Funktionsaufrufe wohl einen Fehler produzieren werden und ersetzen Sie die "-4" in den Fällen, in denen sie nicht in der Definitionsmenge liegt, durch ein Element, das in der jeweiligen Definitionsmenge liegt, so dass keine Fehler mehr produziert werden.
Funktionen kommen in sehr unterschiedlichen Formen vor. Es muss nur immer die Bedingung erfüllt sein, dass jedem Element x einer Menge D eindeutig in ein Element f(x) einer Menge W zugeordnet ist.
Zum Beispiel wird in dieser Tabelle jedem Monat genau 1 Temperatur zugeordnet. Anders herum wird jeder Temperatur genau 1 Monat zugeordnet.
f1: Monat3 → TemperaturMan spricht in diesem Fall auch von Bijunktion oder 1-zu-1 Zuordnung, da es sich um eine Funktion in beide Richtungen handelt.
| Monat3 | Temperatur |
|---|---|
| Jan | 1 |
| Feb | 2 |
| Mar | 5 |
| Apr | 10 |
| Mai | 14 |
| Jun | 17 |
| Jul | 19 |
| Aug | 20 |
| Sep | 15 |
| Okt | 11 |
| Nov | 6 |
| Dez | 3 |
In der folgenden Tabelle kann man weder für jeden Monat eine Temperatur bestimmen (weil es z.B. für den Monat J drei verschiedene Temperaturen gibt), noch kann man jeder Temperatur einen Monat zuordnen, weil es zu der Temperatur 3 zwei verschiedene Monate gibt (F und D). Man sagt für die Beziehung zwischen Monat1 und Temperatur in dieser Tabelle, dass es sich um eine Relation, aber keine Funktion handelt.
| Monat1 | Temperatur |
|---|---|
| J | 1 |
| F | 3 |
| M | 5 |
| A | 10 |
| M | 14 |
| J | 17 |
| J | 19 |
| A | 20 |
| S | 15 |
| O | 11 |
| N | 6 |
| D | 3 |
Die Lösungen zu Aufgaben 1. und 2. stehen weiter unten. Überlegen Sie aber erst, bevor Sie sich die Lösungen anschauen.
1. Bestimmen Sie für die folgenden Graphen (A-F), ob es sich um Funktionen handelt, wenn die Elemente im linken Kreis die Definitionsmenge darstellen und die Elemente im rechten Kreis die Wertemenge.

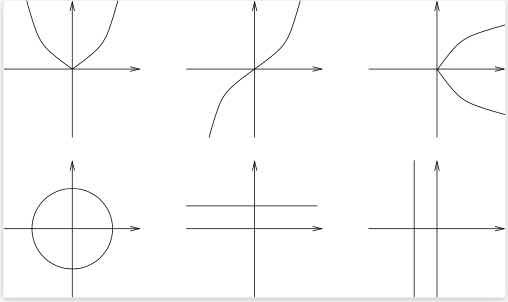
2. Bestimmen Sie für die folgenden Graphen, ob es sich um Funktionen handelt, wenn die waagerechte Achse die Definitionsmenge darstellt und die senkrechte Achse die Wertemenge.
3. Vergleichen Sie nochmal, welche verschiedenen Arten von Funktionen Sie in diesem Kurs gesehen haben (mit reellen Zahlen, Python-Funktionen, Tabellen, Graphen). Wie kann man die Bedingung, dass jedem Element x einer Menge D eindeutig in ein Element f(x) einer Menge W zugeordnet ist, jeweils überprüfen?
Historisch gesehen hat es Jahrhunderte gedauert, bis Funktionen als das mathematische Prinzip erkannt wurden, das diese verschiedenen Darstellungsweisen verbindet. Verzweifeln Sie also nicht, wenn auch Sie etwas Zeit brauchen, bis Sie mit dem Funktionsbegriff in allen Varianten vertraut sind.
1. A) keine Funktion, weil keine eindeutige Zuordnung für Element d. B) ist Funktion. C) keine Funktion, weil keine Zuordnung für Element c. D) ist Funktion und sogar eine Bijunktion. E) keine Funktion, weil keine Zuordnungen. F) keine Funktion, weil keine eindeutige Zuordnung für Elemente d und c.
2. Erste Reihe von links: ist Funktion, ist Funktion (sogar Bijunktion), keine Funktion, weil rechts den Werten der waagerechten Achse jeweils 2 Werte der senkrechten Achse zugeordnet sind. Zweite Reihe von links: keine Funktion, ist Funktion, keine Funktion.